Precise mathematical definitions exist to specify the construction of a triangular array of numbers called Pascal’s Triangle. But they will not be repeated at this point for the benefit of a different view on the nature of that construction, which holds several amazing qualities related to figures and patterns far beyond binomial coefficients.
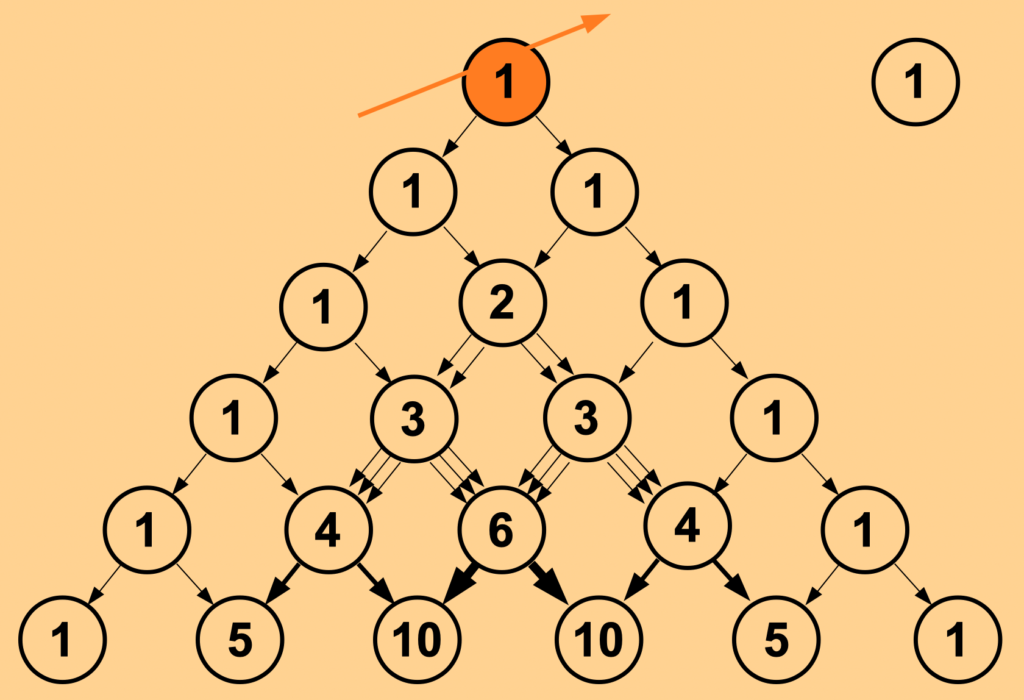
Imagine a first cell, represented here by the figure 1, intending itself to reproduce by means of schizogenesis. The first generation would be the presence of two cells, depicted here by a second row that arises out of the first one.

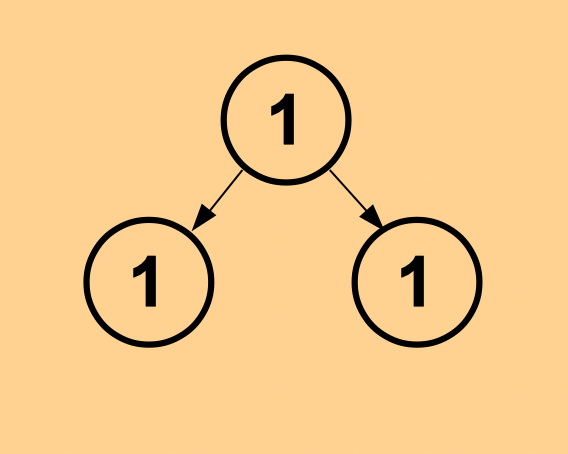
In the next step two cells will again reproduce themselves in the same way to build a second generation of 4 cells, as depicted here in the third row, where the middle position of the triangular representation ‘receives’ a child cell from two parent cells. That procedure can be thought to continue endlessly to construct row by row, and generation by generation, Pascal’s Triangle.
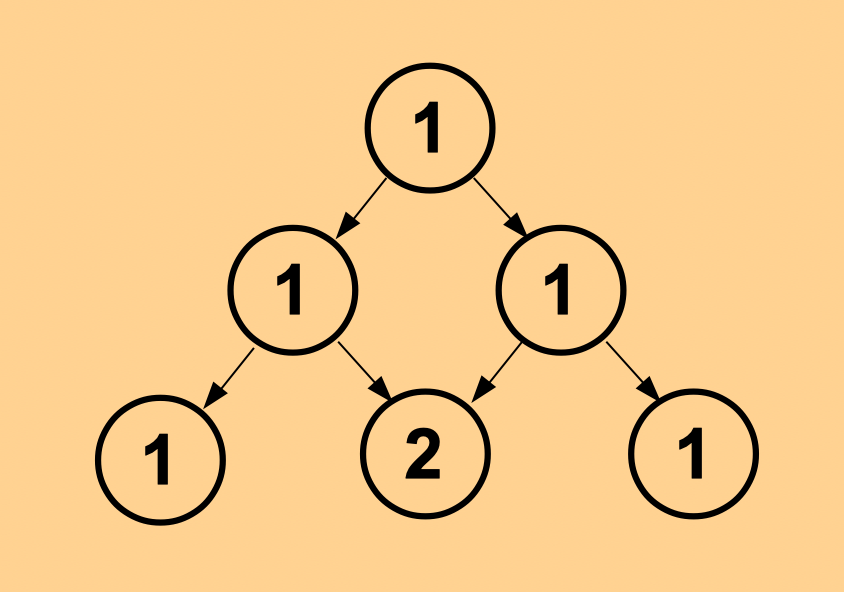
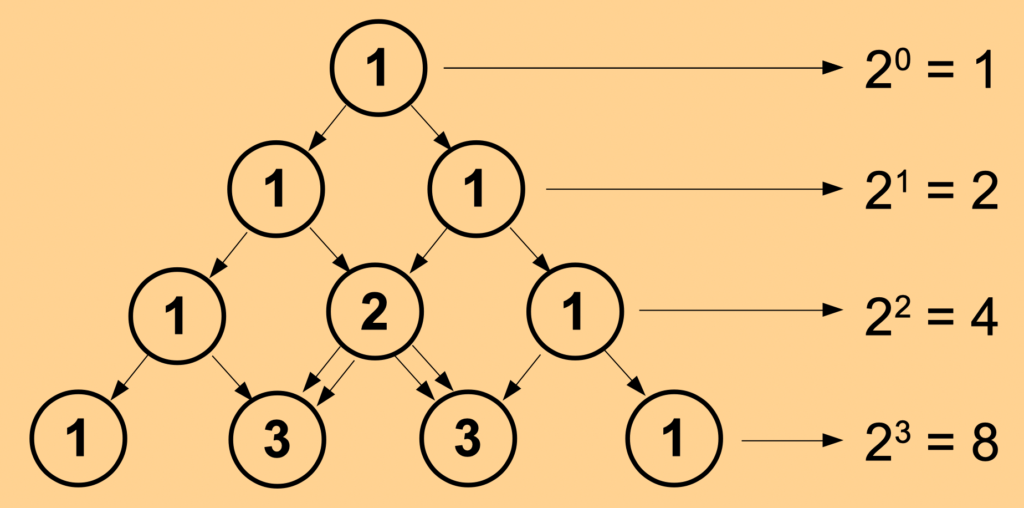
The Number 2
The close affinity of Pascal’s Triangle to the number 2 becomes obvious, as the sum of each row is always resulting in a power of 2 in an ascending order.
The Number 11
The relationship to the number 11 is not as clear as for the number 2, but shows again a remarkable characteristic if it is interpreted as a denominational number system. May be since 11 is the first number having a cross sum of 2?
Each figure in a row is then representing the coefficient of a decimal power in descending order from the left to the right. It shows thereby the quality of the resulting numbers, which are always starting and ending with the digit 1, while being a kind of a palindrome. At least up to the fifth row…
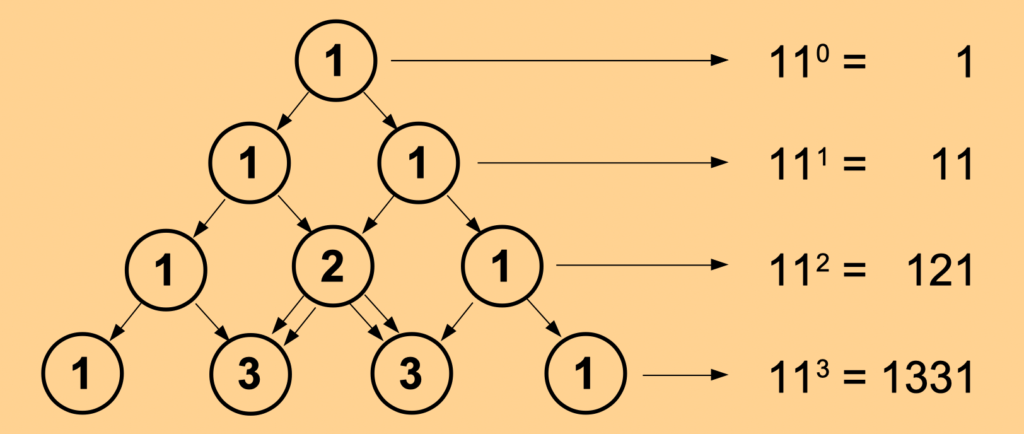
What happens in the sixth row? Well, the system may consistently be continued and will still work, but nevertheless, something changes. The resulting numbers, each a power of 11, lose their quality of being a palindrome, while still starting and ending with the digit 1.
The following equation shall depict the idea of the denominational number system by means of an arithmetical expressions for the sixth row, which is the first exceptional one:

Still each line is representing a power of 11, based on that denominational number system as depicted here.
Sequences of Numbers
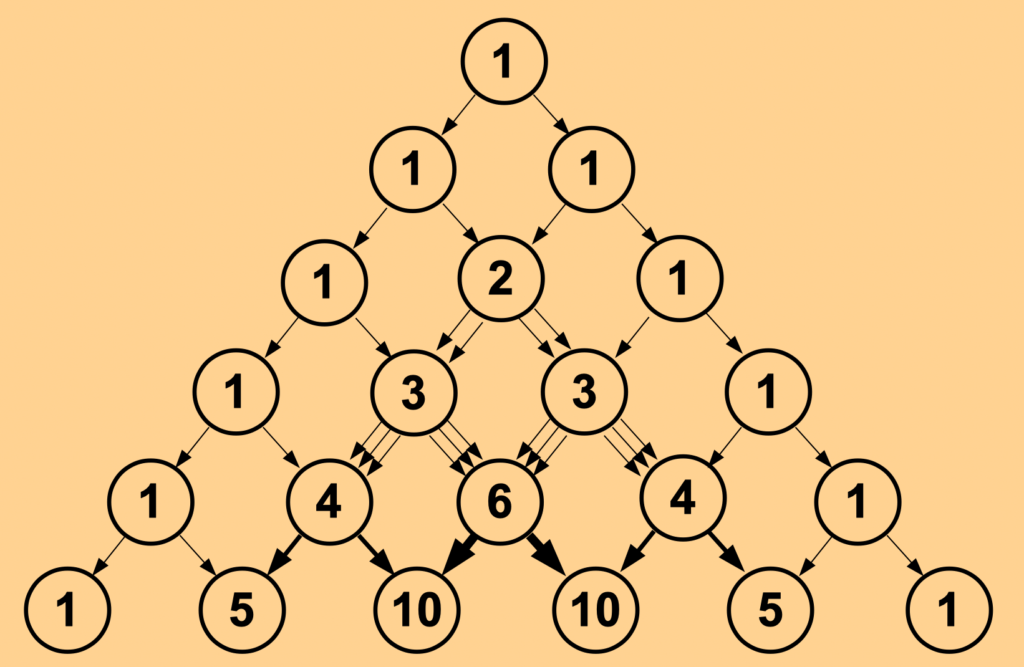
The triangular construct of numbers could also be seen as an aggregation of specific number sequences, arranged in diagonal lines just below the outer edges where all the figures 1 reside. The first diagonal line shows the sequence of natural numbers.
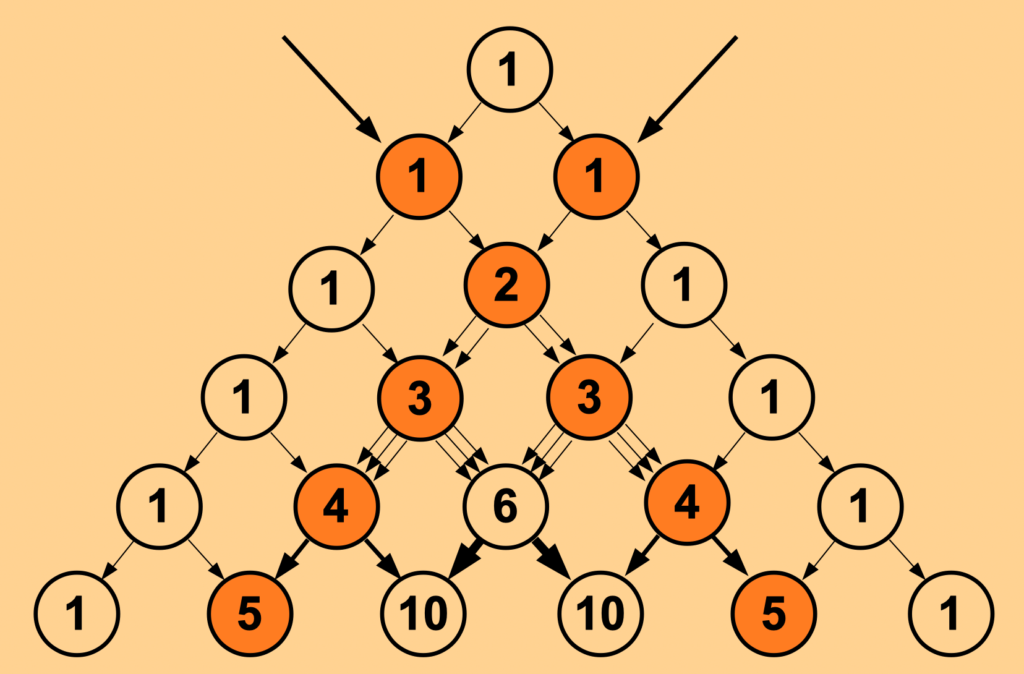
The second diagonal line comprises the triangular numbers.

The third line represents the number of tetrahedral numbers, followed by further sequences of tetrahedral numbers of higher order.
Sierpinski Triangle
A remarkable and well known fractal pattern, called Sierpinski Triangle, appears when separating the elements divisible by 2 from the others. Or in other words, applying two different colours for even and odd numbers.

Prime Numbers
Pascal’s Triangle has also a very special relationship to prime numbers, emerging in two different ways. The first way is related to the numerical quality of specific rows, which are showing a consistent divisibility by a related prime number for all elements between the first and the last element. Trivial for 2 and 3, but not for subsequent primes, and not applicable to other rows.
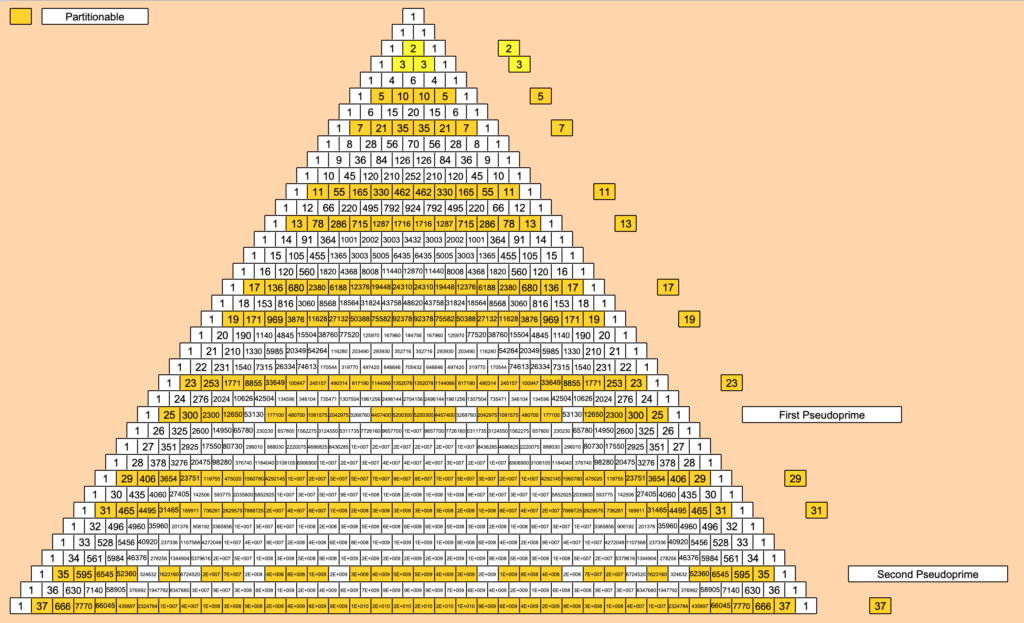
Again the pattern of the ternary grouping of numbers appears in that pattern, where primes are residing on the positions resulting from the equation “6n +/- 1”. In the sixth row (or the fifth generation?) all numbers are divisible by 5, in the eigth row divisible by 7, in the twelfth divisible by 11, and so on. The first row were this relationship fails is row 26, where the first pseudoprime emerges. Still a lot of elements are here divisible by 25, but not all. Nevertheless clearly more than for other rows, again accentuating this specific line.
The second way is showing a very regular pattern, when separating all elements that are divisible by a prime number from the others, depicted below by two different colours. It is showing the result for the number 3.

The edge length of the triangle composed by the minor triangles around the major one is directly related to the applied prime, that is to say of the length “prime – 1”. A property that is better visible in the next example for the number 5.

The same regular pattern appears again and again for higher primes, while other numbers result in more irregular layouts.
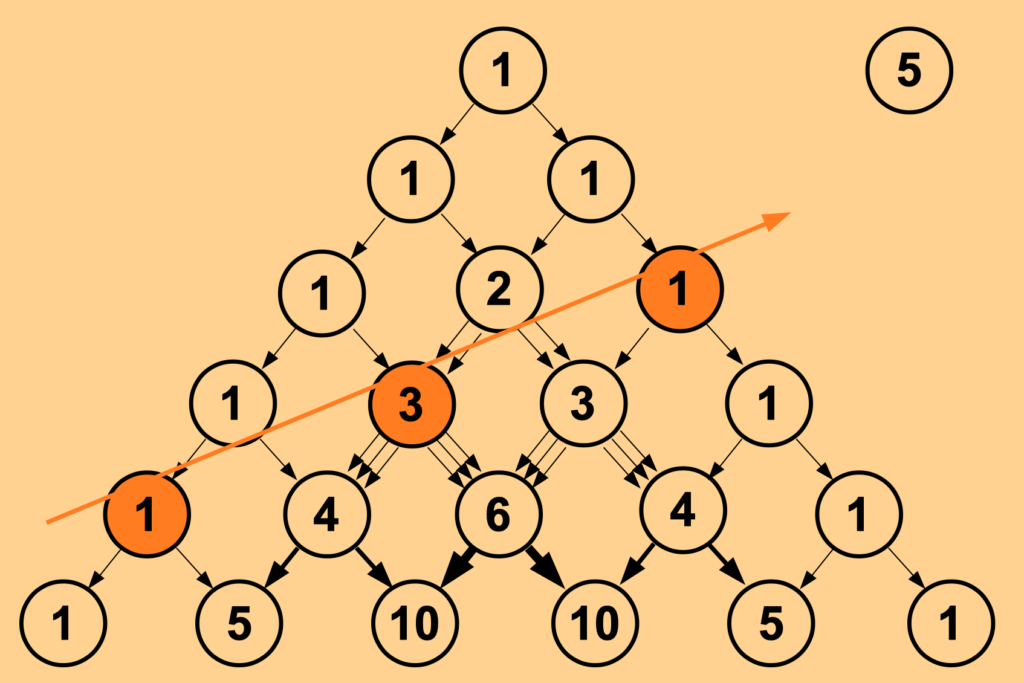
Fibonacci Number
Another very special and well known sequence of numbers is called Fibonacci Numbers. By definition it starts with the two elements 1 and 1, while the following element is always built by the sum of the two preceding ones, resulting in the following sequence:
1, 1, ( 1 + 1 = ) 2, ( 1 + 2 = ) 3, ( 2 + 3 = ) 5, ( 3 + 5 = ) 8, …
The idea behind was to specify a numerical representation for the growths of a rabbit population, and again this specific sequence is hidden in Pascal’s Triangle in the following way.