Besides the classical division of natural numbers into the two sets of even and odd numbers, they can also be split into three equally sized categories, while revealing a totally different view on their nature and interactions. An approach, that is mainly driven by the distribution of prime numbers.

The first group of numbers is residing next to multiples of 6, they are the preceding and succeeding neighbors. Mathematically they can be expressed by the result of the following equation: 6*n +/- 1.

All prime numbers can be found in this set of numbers, except for 2 and 3. The two latter ones have a very specific meaning in this partitioning, that has more to do with a constructive role in relation to the next two groups of numbers than being primes. Also the number 1, which is member of that first group, is taking again a very special role, as it can’t be seen like a prime number, but it is the starting element of that subset.
The number 2 has not more than the two divisors, that are specific to prime numbers: 1, and the number itself. Furthermore it has a very exclusive quality, since it is the only prime number being even. So, can it really be classified as a prime number here?
The number 3 is an odd number and can’t have more than the two divisors 1 and the number itself, since the third potential divisor 2 is specific to even numbers. Again the classification as a prim number is put into question.
The second group of numbers is constructed by and starting with the number 2, comprising all even numbers – except those, that are divisible by 3 and thus part of the third group. Therefore a mathematical expression for those numbers is similar to the first one and could be the following: 6*n +/- 2.

Finally the third group of numbers is constructed by the number 3, comprising the 3 itself and all its multiples. So it can be expressed by the mathematical equation 3*n.

It becomes obvious that the numbers 1, 2, and 3 have a very special meaning within that partitioning, since they are the starting elements in their groups and can be seen as the constructive trinity building the presented subsets of numbers.
The following diagram shows a different way to visualize the idea behind that partitioning: a structure being arranged in concentric circles – what seems to be more natural to depict the nature of those individual groups.
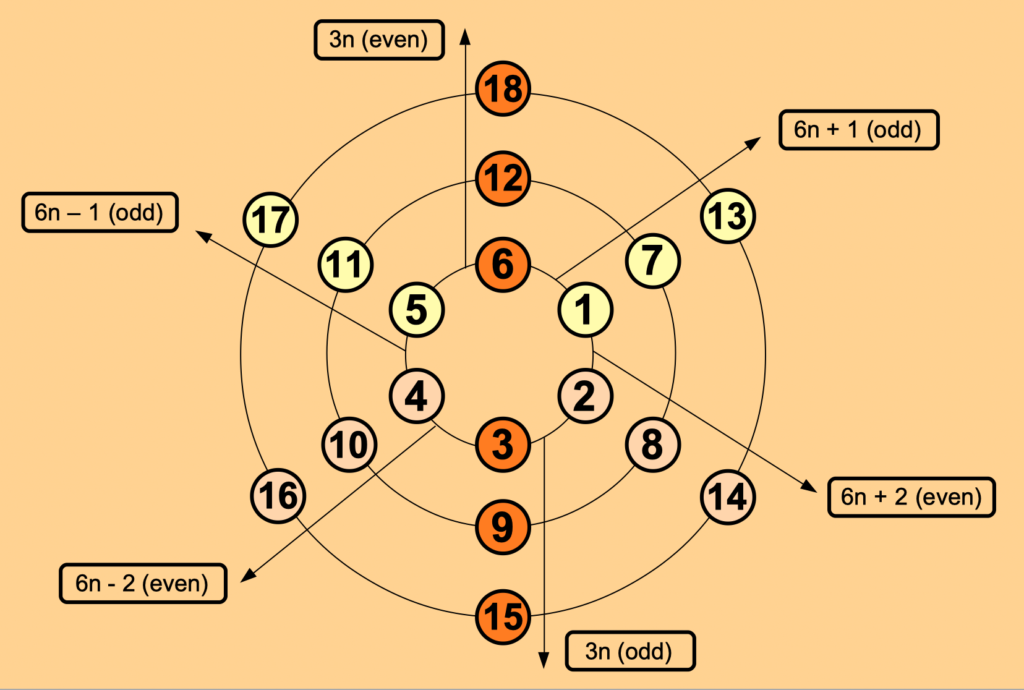
1st Group
The main driver for the given partitioning is the group of immediate neighbors next to the multiples of 6. All prime numbers (greater than 3!) can be found in this pattern, starting with the three well known twin primes 5 and 7, 11 and 13, and 17 and 19. Up to the number 24 a perfect world can be found here, but starting with the number 25 this arrangement fails.

25 is the first number within this group, that is not fulfilling the definition of primes. Besides 1 and itself it is divisible by 5 and thus starting to split this group of numbers into two further subsets: primes and pseudoprimes.Still all numbers of that group are definitely odd.
Arithmetical operations reveal here two distinct behaviors. For addition and subtraction the numbers of that group project themselves to one of the two others. For multiplication and division they remain in their group, as long as the division is possible within the set of natural numbers.
element of group 1 + element of group 1 = element of group 2 or 3
element of group 1 – element of group 1 = element of group 2 or 3
element of group 1 * element of group 1 = element of group 1
element of group 1 / element of group 1 = element of group 1, or no result
The third equation gives already the hint, that not all numbers of the first group can be prime. Some of them are composites, having at least one number out of that group as a divisor, so that they must be “pseudoprime” as a consequence.
2nd Group
The second group has a similar distribution pattern of numbers as the first one, but slightly shifted. Again they build a kind of pairs around another number at every sixth position, but with an offset of three positions compared to the first group.

Arithmetical operations show a more or less open group of numbers, that is able to project into the other groups. Addition and subtraction remains in the same group, or goes to the third group, while for multiplications the result remains within the same group. Division can’t project numbers into the third group, but into the two others, for solutions existing in the set of natural numbers. It gives here already the hint that numbers of the second group might be purely expressed by prime factors.
element of group 2 + element of group 2 = element of group 2 or 3
element of group 2 – element of group 2 = element of group 2 or 3
element of group 2 * element of group 2 = element of group 2
element of group 2 / element of group 2 = element of group 1 or 2, or no result
3rd Group
The third group of figures is based on the number 3 and comprises all its multiples. Correspondingly it can be split into the two equally sized subsets of even and odd numbers, as can be seen in the last picture of the first paragraph. The vertical axis of numbers is highlighting exactly that group, where the lower part is showing the odd numbers, and the upper part the even numbers.

Having a look on the relation to arithmetical operations reflects here an almost closed group of numbers. it opens itself only with the division towards other groups, if the division is possible within the set of natural numbers.
element of group 3 + element of group 3 = element of group 3
element of group 3 – element of group 3 = element of group 3
element of group 3 * element of group 3 = element of group 3
element of group 3 / element of group 3 = any element, or no result